automata: Simulation and manipulation

Automata are abstract machines used to represent models of computation, and are a central object of study in theoretical computer science. Given an input string of characters over a fixed alphabet, these machines either accept or reject the string. A language corresponding to an automaton is the set of all strings it accepts. Three important families of automata in increasing order of generality are the following:

1. Finite-state automata
2. Pushdown automata
3. Turing machines

The automata package facilitates working with these families by allowing simulation of reading input and higher-level manipulation of the corresponding languages using specialized algorithms. For an overview on automata theory, see this Wikipedia article, and for a more comprehensive introduction to each of these topics, see these lecture notes.

Statement of need

Automata are a core component of both computer science education and research, seeing further theoretical work and applications in a wide variety of areas such as computational biology and networking. Consequently, the manipulation of automata with software packages has seen significant attention from researchers in the past. The similarly named Mathematica package Automata implements a number of algorithms for use with finite-state automata, including regular expression conversion and binary set operations. In Java, the Brics package implements similar algorithms, while the JFLAP package places an emphasis on interactivity and simulation of more general families of automata.

automata serves the demand for such a package in the Python software ecosystem, implementing algorithms and allowing for simulation of automata in a manner comparable to the packages described previously. As a popular high-level language, Python enables significant flexibility and ease of use that directly benefits many users. The package includes a comprehensive test suite, support for modern language features (including type annotations), and has a large number of different automata, meeting the demands of users across a wide variety of use cases. In particular, the target audience is both researchers that wish to manipulate automata, and for those in educational contexts to reinforce understanding about how these models of computation function.

Package features

The API of the package is designed to mimic the formal mathematical description of each automaton using built-in Python data structures (such as sets and dicts). This is for ease of use by those that are unfamiliar with these models of computation, while also providing performance suitable for tasks arising in research. In particular, algorithms in the package have been written for tackling performance on large inputs, incorporating optimizations such as only exploring the reachable set of states in the construction of a new finite-state automaton. The package also has native display integration with Jupyter notebooks, enabling easy visualization that allows students to interact with automata in an exploratory manner.

Of note are some commonly used and technical algorithms implemented in the package for finite-state automata:

• An optimized version of the Hopcroft-Karp algorithm to determine whether two deterministic finite automata (DFA) are equivalent.

• The product construction algorithm for binary set operations (union, intersection, etc.) on the languages corresponding to two input DFAs.

• Thompson’s algorithm for converting regular expressions to equivalent nondeterministic finite automata (NFA).

• Hopcroft’s algorithm for DFA minimization.

• A specialized algorithm for directly constructing a state-minimal DFA accepting a given finite language.

• A specialized algorithm for directly constructing a minimal DFA recognizing strings containing a given substring.

To the authors’ knowledge, this is the only Python package implementing all of the automata manipulation algorithms stated above.

Example usage

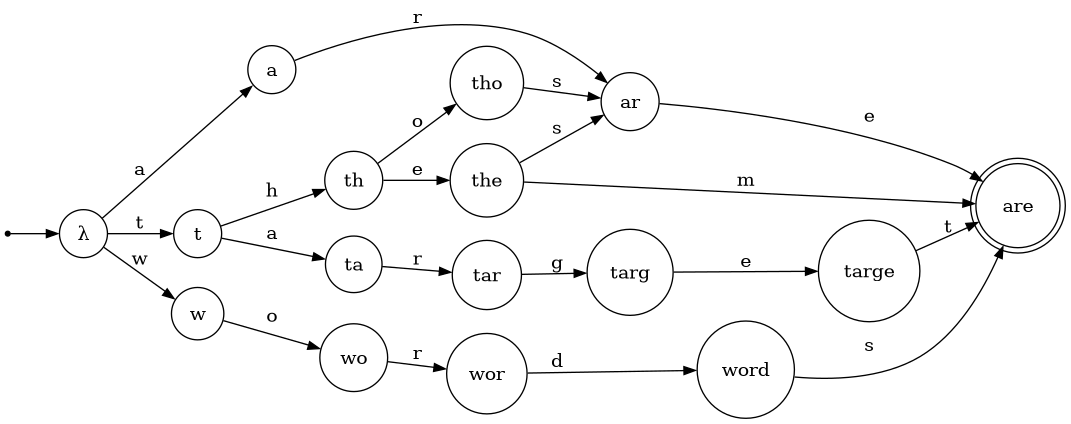
The following example is inspired by the use case described in this blog post. We wish to determine which strings in a given set are within the target edit distance to a reference string. We will first initialize a DFA corresponding to a fixed set of target words over the alphabet of all lowercase ascii characters.

from automata.fa.dfa import DFA
from automata.fa.nfa import NFA
import string

target_words_dfa = DFA.from_finite_language(
  input_symbols=set(string.ascii_lowercase),
  language={'these', 'are', 'target', 'words', 'them', 'those'},
)

Next, we construct an NFA recognizing all strings within a target edit distance of a fixed reference string, and then immediately convert this to an equivalent DFA. The package provides builtin functions to make this construction easy, and we use the same alphabet as the DFA that was just created.

words_within_edit_distance_dfa = DFA.from_nfa(
  NFA.edit_distance(
    input_symbols=set(string.ascii_lowercase),
    reference_str='they',
    max_edit_distance=2,
  )
)

Finally, we take the intersection of the two DFAs we have constructed and read all of the words in the output DFA into a list. The library makes this straightforward and idiomatic.

found_words_dfa = target_words_dfa & words_within_edit_distance_dfa
found_words = list(found_words_dfa)

The DFA found_words_dfa accepts strings in the intersection of the languages of the DFAs given as input, and found_words is a list containing this language. Note the power of this technique is that the DFA words_within_edit_distance_dfa has an infinite language, meaning we could not do this same computation just using the builtin sets in Python directly (as they always represent a finite collection), although the syntax used by automata is very similar to promote intuition.

Citing

This post is adapted from our JOSS paper, which should be used for citations.